2 kwietnia 2019r. Polskie Towarzystwo Matematyczne obchodzi setną rocznicę powstania. Z tej okazji 243 uczniów naszej szkoły na boisku zbudowało Fraktal Sierpińskiego - fraktal na stulecie. Inicjatorką i główną koordynatorką przedsięwzięcia w naszej szkole była pani Maria Bieniecka wspierana przez pozostałe nauczycielki matematyki oraz nauczycieli i wychowawców klas.
Uczniowie klas 3-6 oraz jednej z klas 7 dzielnie starali się dostosować się do instrukcji konstruowania fraktala.
Mamy nadzieję, że za rok zbudujemy jeszcze dokładniejszy :-)
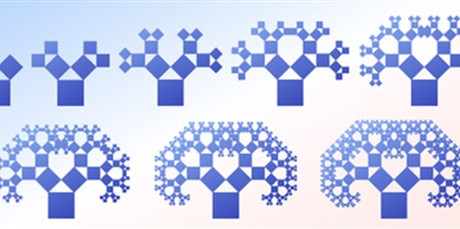
Fraktal jest w uproszczeniu obiektem samopodobnym, czyli takim, którego fragmenty wykazują podobieństwo do całości.
Fraktal może być złożony tylko z odcinków, trójkątów czy kwadratów. Może też być bardzo złożoną, trudną do opisania matematycznie figurą.
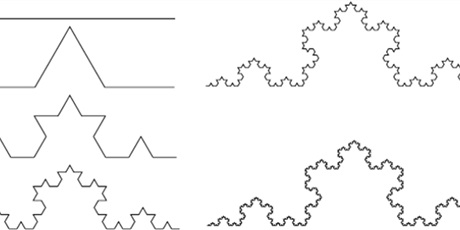
Fraktal zwany Krzywą Kocha powstaje przez dorysowywanie kolejnych odcinków w odpowiednich miejscach. Została ona opisana po raz pierwszy przez Helgego von Kocha w roku 1904 r. Po połączeniu sześciu krzywych otrzymujemy „płatek śniegu” z powtarzającą się, skomplikowaną linią brzegową.
Trójkąt Sierpińskiego otrzymujemy w następujący sposób: w trójkącie równobocznym łączymy środki krawędzi dzieląc go w ten sposób na mniejsze trójkąty. Trójkąt środkowy usuwamy, a w pozostałych trzech trójkątach operację powtarzamy. W wyniku takiego powtarzania otrzymujemy 3, 9, 27, 81, 243... trójkąty. Każdy z nich jest dokładną wersją trójkątów z poprzednich kroków.
Dywan Sierpińskiego to fraktal otrzymany z kwadratu za pomocą podzielenia go na dziewięć mniejszych kwadratów, usunięcia środkowego kwadratu i ponownego zastosowania tej samej procedury do każdego z pozostałych ośmiu kwadratów.
Fraktale są ciekawe, piękne... i wykorzystywane przez naturę.
Zdjęcia wykonał pan Jan Bielawski - serdecznie dziękujemy!